Konkurs z matematyki "Kangura" - 2000 - STUDENT - Litwa

---

Janek Wędrowniczek wyjechał samochodem z miasta A i jechał kolejno 10 km na północ, 10 km na wschód, 6 km na południe, 2 km na zachód, 8 km na północ, 4 km na zachód i 9 km na południe ko cząc w ten sposób podróż w mieście B. Jakaj jest odległość w linii prostej pomiędzy miastami A i Bl

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Od poniedziałku do środy Marek zawsze kłamie, w pozostałe zaś dni tygodnia mówi prawdę. Pewnego dnia Marek spotkał Marię i powiedział:
1)„Wczoraj kłamałem."
2)„Od pojutrza przez dwa kolejne dni będę kłamał." W jakim dniu Marek spotkał Marię?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Średnia wieku rodziców Joanny wynosi 39 lat, przy czym ojciec jest o 4 lata starszy od matki. Średnia wieku Joanny i jej ojca wynosi 23 lata. Ile lat ma Joanna?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Reszta z dzielenia liczby 3²⁰ • 5³⁰ - 2 przez 15 jest równa 

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Pająk idzie od punktu A do punktu B po powierzchni walca. Jaka jest długość najkrótszej drogi, którą musi pokonać pająk, aby dojść z punktu A do punktu B, jeżeli (patrz rysunek) r = 1, h = 6?
 

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Jedyna liczba naturalna n, dla której zachodzi równość
[( + 1) • ( - 1) + 1]^0,25 = 256
należy do zbioru

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Statek kosmiczny leci z Ziemi do odległej о 2²⁰ km planety X. Gdy statek przebył 1/4 drogi, utracił kontakt radiowy z Ziemią. Kontakt ten odzyskał w odległości 2¹⁹ km od Ziemi. Ile kilometrów leciał bez kontaktu radiowego?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Największy wspólny dzielnik liczb naturalnych x i у jest równy 1 oraz xy = 300. He co najmniej może wynosić suma x + yl

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Niech xyz oznacza liczbę trzycyfrową, gdzie x jest cyfrą setek, у cyfrą dziesiątek i z cyfrą jedności. Załóżmy, że x > z > 0 i że cyfrą setek liczby n = xyz - zyx jest 4. Wówczas cyfry dziesiątek i jedności liczby N są odpowiednio równe

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Dodatnia liczba całkowita a ma tę własność, że suma
a + 2a + За + Aa + 5a + 6a + la + 8a + 9a
zapisana w dziesiątkowym systemie pozycyjnym składa się z jednakowych cyfr. Jaka to cyfra?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Rysunek przedstawia trójkąt ABC z wpisanym okręgiem к o środku w punkcie S, przy czym D, E i F są punktami styczności okręgu k z bokami trójkąta ABC. Ile wynosi miara kąta D F E, jeżeli kąt DAE ma miarę 32°?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Mietek oszcędza, aby kupić komputer, który kosztuje 5400 zł. Zapytany, ile już zgromadził pieniędzy, odpowiedział: „Nawet gdybym miał o jedną piątą więcej niż mam, brakowałoby mi jeszcze o jedną czwartę mniej niż w rzeczywistości brakuje." Ile pieniędzy miał Mietek?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Pewien n-kąt wypukły ma dokładnie 6n przekątnych. Ile wynosi ni

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

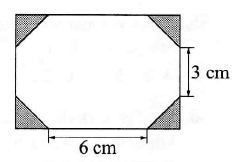
Odcinając od rogów prostokąta cztery identyczne trójkąty równoramienne, otrzymujemy ośmiokąt o powierzchni 62 cm2 (patrz rysunek). Jaka jest łączna powierzchnia odciętej części?
 

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Jeżeli 2¹⁹⁹⁴ + 4⁹⁹⁷ + 8⁶⁶⁵ = 16^х, to x = 

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Bartosz powinien pomnożyć dwie dwucyfrowe liczby naturalne. Niestety, pomylił się i przemnożył pierwszą z nich przez liczbę powstałą przez zamianę kolejności cyfr liczby drugiej. Otrzymany wynik był o 3816 większy od właściwego. Jaki powinien być właściwy wynik?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Przedstawiony na rysunku obok wielokąt R zbudowany jest z 6 kwadratów o polu 1 cm² każdy. Wybieramy jeden spośród punktów A, B, C, D, E jako środek symetrii i konstruujemy obraz R' wielokąta R w symetrii środkowej względem wybranego punktu. Który spośród punktów A, B, C,D, E należy wybrać aby pole figury RUR' było równe 8 cm^{2 ?}


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Na płaszczyźnie dany jest kwadrat o boku 1. Ile punktów płaszczyzny leży w jednakowej odległości od dwóch sąsiednich wierzchołków kwadratu i w odległości 1 od jednego z pozostałych wierzchołków?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Miasta A i В leżą w różnych strefach czasowych. Samolot lecący z A do В startuje o godzinie 6⁰⁰ w poniedziałek i ląduje о 14⁰⁰ we wtorek. W drodze powrotnej startuje z В о 13⁰⁰ w czwartek i ląduje о 15⁰⁰ w czwartek (wszędzie czasu lokalnego), przy czym samolot leci w obie strony z tą samą prędkością. Jeżeli w A jest sobota, godzina 16⁰⁰, to w В jest

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Rozważmy sześcian o krawędzi 2 i sferę G o środku w środku symetrii sześcianu. Niech К oznacza powierzchnię sześcianu. Zbiór KDG składa się z sześciu okręgów wtedy i tylko wtedy, gdy promie r sfery spełnia nierówności

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Jeżeli x,y ε R spełniają warunek x² + y² = 1, to największą wartością iloczynu xy jest liczba

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Sonda kosmiczna po wylądowaniu na Marsie odkryła tam wioskę zamieszkaną przez Marsjan. Załoga sondy stwierdziła, że Marsjanie mają 1 m wzrostu, każdy jest albo czerwony, albo zielony, albo niebieski, każdy z nich ma od 2 do 5 rąk, z ich głów zaś wyrasta od 3 do 20 małych antenek.
Ilu co najmniej mieszka ców powinna liczyć ta wioska, aby można było z całą pewnością wybrać spośród jej mieszka ców 11 identycznie wyglądających osobników do drużyny piłki nożnej w meczu przeciwko drużynie Ziemi? (Cała jedenastka Marsjan powinna być w jednym kolorze, każdy z tą samą liczbą rąk i każdy z tą samą liczbą antenek.)

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Ile dodatnich rozwiąza ma poniższe równanie,?



Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Na ile sposobów można liczbę 447 przedstawić w postaci sumy kolejnych liczb nieparzystych?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Dziesięciu chłopców chce grać w koszykówkę. Na ile sposobów mogą podzielić się na dwie pięcioosobowe drużyny, jeżeli Mirek chce grać w jednej drużynie ze Zbyszkiem, natomiast Paweł nie chce grać w jednej drużynie z Danielem''

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

W trójkącie ABC (patrz rysunek) mamy ∠CAB = 30°, ∠CBA = 120°, CD jest dwusieczną kąta ACB. Wtedy
   równa się


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Ile jest dodatnich liczb całkowitych, których największy dzielnik właściwy (tzn. dzielnik rożny od 1 i od danej liczby) wynosi 91?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Jeżeli p(ri) oznacza iloczyn cyfr liczby naturalnej n, to
p(1)+ p(2) + р(3) + • • • + р(100)
 jest równe 

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Na wadze szalkowej wyznacza się wagę przedmiotu w ten sposób, że na jednej szalce kładziemy ważony przedmiot, na drugiej zaś lub na obydwu szalkach odważniki, starając się doprowadzić wagę do pozycji równowagi. Chcemy wyznaczać wagi przedmiotów o ciężarze wyrażającym się całkowitą liczbą gramów od 1 do 10 włącznie. Jaka minimalna liczba odważników jest do tego celu potrzebna^

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Dany jest czworościan ABCD. Liczba płaszczyzn położonych w jednakowej odległości od wszystkich czterech wierzchołków czworościanu wynosi

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija