Konkurs z matematyki "Kangura" - 2001 - KADET - Litwa
Klausimas #1
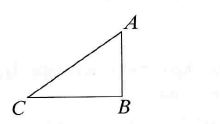
Arkusz papieru ma kształt trójkąta prostokątnego o długości boków 3, 4 i 5. Jeżeli będziemy zginać ten trójkąt wzdłuż linii prostej w ten sposób, że punkt С pokryje się z punktem В, a potem powtórzymy ten proces w taki sposób, że punkt A pokryje się z punktem B, to otrzymany wielokąt będzie
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #2
Robert chce zapakować niebieskie oraz czerwone kangurki, układając je po 10 w każdym pudełku. Ma on 178 kangurków jednego i 121 kangurków drugiego koloru. Ile pudełek potrzeba mu do zapakowania wszystkich kangurków tak, aby w każdym pudełku były kangurki tylko jednego koloru?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #3
Który pierście należy przeciąć, aby pozostałe pierścienie oddzielili się jeden od drugiego?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #4
W klasie Edka chłopców jest o 7 więcej niż dziewcząt. Liczba chłopców w jego klasie jest dwa razy większa od liczby dziewcząt. Ile koleżanek ma w klasie jego przyjaciółka Janka z tej samej klasy?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #5
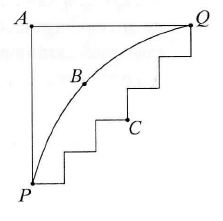
Rysunek przedstawia kilka ulic miasteczka. Odległości od Л do P oraz od A do Q są równe 500 m. Odległość od P do б przez punkt A jest o 215 metrów większa niż odległość przez punkt B. Wówczas odległość od P do Q przez punkt С w porównaniu z odległością od P do Q przez В jest
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #6
Spośród liczb —9, —7, —5, 2, 4 i 6 wybrano dwie liczby, które potem pomnożono. Najmniejszy możliwy iloczyn tych liczb wynosi
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #7
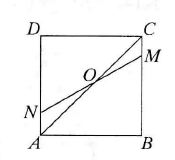
Figura ABCD jest kwadratem. Wyznacz wielkość kąta СОМ, jeżeli ZOND = 60°.
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #8
Mała koala objada liście z jednego eukaliptusa w ciągu 10 godzin. Jej tata i mama jedzą dwa razy szybciej. W ciągu jakiego czasu ta trzyosobowa rodzina obje wszystkie liście z jednego eukaliptusa?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #9
Bok sześciokąta foremnego równa się 1, a bok trójkąta foremnego równa się 3. Jaki jest stosunek pól sześciokąta i trójkąta?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #10
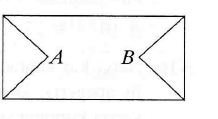
Ile jest różnych dróg, prowadzących od punktu A do punktu В w tej figurze, pod warunkiem, że każdy punkt można przeciąć nie więcej niż jeden raz?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #11
Na płaszczyźnie umieszczono kwadrat o boku długości 1 cm. Każdy wierzchołek tego kwadratu jest równocześnie środkiem okręgu o promieniu 1 cm, znajdującego się na tej samej płaszczyźnie. He jest punktów, w których przecinają się co najmniej dwa okręgi?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #12
Na każdym z dwóch stołów leży w szeregu 2001 orzechów. Gaweł bierze orzechy z pierwszego stołu. Najpierw bierze co trzeci orzech; potem bierze co piąty z pozostałych orzechów. Paweł bierze orzechy z drugiego stołu. Najpierw bierze co piąty orzech; potem z pozostałych orzechów bierze co trzeci. Które z następujących stwierdze jest słuszne?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #13
W równości 4 x KLMNPA = 4KLMNP każdej z liter K, L, M, N, P odpowiada cyfra. Jaka cyfra odpowiada literze Ml
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #14
ABC jest trójkątem równobocznym, В zaś jest środkiem odcinka AD. Punkt E obrano w taki sposób, że DE = AB. Wiadomo, że odległość między C i E jest możliwie największa. Jaka jest wielkość kąta BED1
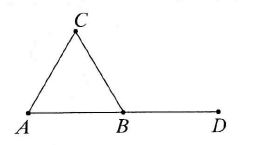
Taškas E paimtas taip, kad DE = AB. Yra žinoma, kad atstumas tarp C ir £ yra didžiausias galimas. Kam lygus kampas BEDI
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #15
24-godzinowy zegar elektroniczny pokazuje godziny (2 cyfry) oraz minuty (2 cyfry). Ile razy od jednej minuty po północy (00:01) do jednej minuty przed północą (23:59) zegar pokaże taki czas, który się nie zmienia przy czytaniu od początku i od ko
ca (na przykład 15:51)?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #16
Nawet gdy wielbłąd Chęć jest spragniony, to 84% jego wagi stanowi woda. Gdy ugasi pragnienie, jego waga zwiększa się do 800 kg, a woda stanowi 85% jego masy. Ile waży wielbłąd Chęć, gdy jest spragniony?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #17
Jacek oraz Wacek wspólnie trenują. Każdy z nich biegnie ze stałą prędkością. Jacek potrzebuje 12 minut na pokonanie 5 kręgów, Wacek zaś odpowiednio 10 minut na pokonanie 3 kręgów. Wystartowali jednocześnie. Ile kręgów pokonają razem do chwili, gdy obaj znów znajdą się razem na linii startu?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #18
Na rysunku ∠A = ∠B = 90°, a SABCD : SACB = 3.
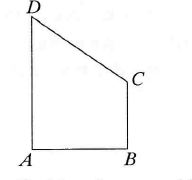
Ile wynosi stosunek SADB : SACB
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #19
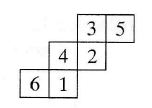
Rysunek obok przedstawia siatkę sześcianu, na którego ścianach napisano liczby od 1 do 6. Mnożymy 3 liczby znajdujące się na takich trzech ścianach, które schodzą się przy jednym wierzchołku sześcianu. Wyznacz największy możliwy iloczyn takich liczb.
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #20
Rybak sporządził prostokątną sieć. We wnętrzu ma ona 32 węzły. Do brzegów sieci rybak przymocował 28 spławików. Ile oczek ma sieć?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #21
Ile kawałków nie można otrzymać po przekrojeniu płaskiego okrągłego tortu czterema prostymi cięciami od brzegu do brzegu?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #22
W zawodach kangurowych w skokach każdy zawodnik wykonuje pięć skoków. Za każdy skok można uzyskać od 1 do 20 punktów. Gdy zawodnik wykona wszystkie skoki, jego najgorszy wynik (lub jeden z jego najgorszych wyników, jeśli najmniejszą jednakową liczbę punktów uzyskał za kilka skoków) nie zalicza się do sumy kocowej. Przed odjęciem najniższej oceny Joasia za pięć skoków uzyskała 72 punkty. Jaki może być najmniejszy jej wynik ostateczny?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #23
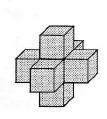
Małgosia zrobiła sobie talizman z siedmiu kostek do gry, sklejając je w taki sposób, że każda para przylegających do siebie ścianek ma równą liczbę oczek. Pewnego razu podczas zabawy talizman wpadł do puszki z farbą i oczek na ściankach, niestety, więcej nie widać. Ile oczek było na początku na całej powierzchni talizmanu?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #24
Jaka jest pierwsza cyfra najmniejszej liczby naturalnej, której suma wszystkich cyfr wynosi 2001?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #25
Na rysunku przedstawiono widok z lewej strony oraz widok z przodu pewnej konstrukcji złożonej z klocków sześciennych. Z jakiej najmniejszej i z jakiej najwięk¬szej liczby klocków może się składać ta konstrukcja?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #26
Niektóre z 11 dużych pudełek zawierają po 8 średnich pudełek, niektóre zaś z tych średnich pudełek zawierają po 8 małych pudełek. Wiadomo, że pustych pudełek jest 102. Jaka jest liczba wszystkich pudełek?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #27
Piłka nożna uszyta jest z czarnych i białych kawałków skóry. Czarne kawałki są pięciokątami foremnymi, białe zaś - sześciokątami foremnymi. Każdy pięciokąt jest otoczony pięcioma sześciokątami, a każdy sześciokąt jest otoczony trzema pięciokątami oraz trzema sześciokątami. Piłka ma dwanaście czarnych pięciokątów. He białych sześciokątów ma ta piłka?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #28
Iloczyn wieków wszystkich dzieci w rodzinie wynosi 1664. Najstarsze dziecko jest dwa razy starsze od najmłodszego. Ilu jest dzieci w rodzinie?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #29
W klasie uczy się 10 chłopców. W sobotę odbędzie się ciekawy mecz. Iloma różnymi sposobami da się utworzyć z nich grupę kibiców na ten mecz, jeżeli wiadomo, że Łukasz, jeżeli tylko pójdzie na mecz, koniecznie zabierze ze sobą Macieja? (Grupa składa się co najmniej z dwu chłopców.)
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #30
Andrzej i Bartosz grają w taką grę. Po kolei biorą kamyczki ze stosu leżącego na stole, za jednym razem nie więcej niż 7. Nie wolno wziąć tyle kamyczków, ile ich wziął ostatnim razem drugi uczestnik. Przegrywa ten, kto nie może zrobić kolejnego posunięcia. Na początku gry w stosie jest 20 kamyczków. Ile kamyczków powinien wziąć rozpoczynając grę Andrzej, jeśli chce wygrać?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5





