Konkurs z matematyki "Kangura" - 2003 - Kadet - Litwa
Klausimas #1
W sklepie zoologicznym było 5 papug. Ich średnia cena była równa 6000 zł. Pewnego dnia najpiękniejsza z tych papug została sprzedana. Średnia cena pozostałych 4 papug była równa 5 000 zł. Jaka była cena sprzedanej papugi?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #2
Złożona serwetka została nacięta tak, jak to pokazuje zamieszczony obok rysunek. Jak będzie ta serwetka wyglądała po rozłożeniu?
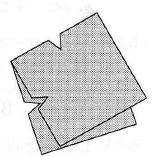
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #3
Z 16 małych kwadracików ułożono kwadrat. Ile co najwyżej tych kwadracików podzielonych może zostać na dwie części przez jedną prostą?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #4
Pole koła drewnianego, przedstawionego na rysunku, wynosi a, a pole kwadratu drewnianego wynosi b. Opasamy trzy takie koła nie poruszając ich nicią możliwie najmniejszej długości.

Jakie pole obejmie nić?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #5
Ile co najwyżej wewnętrznych kątów prostych może mieć sześciokąt (niekoniecznie wypukły)?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #6
Łączna pojemność butelki i szklanki jest równa pojemności dzbanka. Pojemność butelki jest równa łącznej pojemności szklanki i kufla. Łączna pojemność trzech kufli jest równa łącznej pojemności dwóch dzbanków. Ile szklanek ma łączną pojemność jednego kufla?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #7
Diagram, przedstawiony na rysunku, jest złożony z 44 pól 1 x 1. Na ile sposobów można pokryć wszystkie 40 jego białych pól 20 prostokątnymi kostkami 1 x 2? (Diagramu nie wolno obracać. Dwa pokrycia uważa się za różne, jeżeli choć jedna kostka jest położona inaczej.)

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #8
W liczbie, która miała co najmniej dwie cyfry, wykreślono ostatnią cyfrę. Otrzymana liczba była и razy mniejsza od poprzedniej. Jaka jest największa możliwa wartość n?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #9
Narysowane są cztery odcinki. Ile punktów przecięcia nie mogą oni mieć?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #10
Która z poniższych liczb po pomnożeniu przez 768 da w wyniku iloczyn zakończony największą liczbą zer?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #11
Na stole leży kwadratowa przezroczysta folia z napisaną literą y. Obracamy tę folię o 90° zgodnie z ruchem wskazówek zegara, następnie odwracamy ją wokół lewej krawędzi i wreszcie obracamy o 180° w kierunku przeciwnym do ruchu wskazówek zegara. Co zobaczymy teraz?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #12
Michaś ma 42 identyczne sześcienne klocki, każdy o krawędzi długości 1 cm. Ze wszystkich tych klocków zbudował pełny prostopadłościan, którego obwód podstawy jest równy 18 cm. Jaka jest wysokość zbudowanego prostopadłościanu?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #13
Mirek wystrzelił po trzy strzały do każdej z czterech identycznych tarcz (patrz rysunek poniżej). Na pierwszej (patrząc od lewej strony) tarczy uzyskał 29, na drugiej 43, na trzeciej 47 punktów. Ile punktów uzyskał na czwartej tarczy?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #14
Pusta ciężarówka waży 2000 kg. Rano, po załadowaniu towaru, ładunek stanowił 80% masy załadowanej ciężarówki. U pierwszego z odbiorców towaru rozładowano czwartą część ładunku. Jaki procent masy załadowanej ciężarówki stanowił wówczas ładunek?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #15
Jaka jest powierzchnia zacieniowanego obszaru na rysunku obok, jeżeli promień okręgu wynosi 3?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #16
Mamy do dyspozycji 6 odcinków o długościach: 1, 2, 3, 2001, 2002, 2003. Na ile sposobów można wybrać spośród nich takie trzy, które utworzą trójkąt?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #17
Ile dodatnich liczb całkowitych n ma tę własność, że spośród dodatnich dzielników liczby n, różnych od 1 i od n, największy jest 15 razy większy od najmniejszego?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #18
Na prostej zaznaczonych jest kolejno od lewej do prawej sześć punktów K, L, M, N, P, R, w takiej właśnie kolejności. Jeżeli KN = M R oraz LN = NR, to koniecznie
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #19
Paweł ma sześć kartek, na każdej z nich napisana jest liczba naturalna. Paweł wybrał trzy spośród nich i obliczył sumę napisanych na nich liczb. W podobny sposób policzył wszystkie 20 możliwych sum odpowiadających 20 możliwym wyborom trzech kartek. Zauważył wówczas, że 10 sum to 16, 10 pozostałych to 18. Jaka była najmniejsza liczba spośród napisanych na sześciu kartkach?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #20
Paweł, Zbyszek, Mirek, Piotruś i Mietek stoją w kole, przy czym odległości pomiędzy każdymi dwoma stojącymi obok siebie chłopcami są różne. Następnie każdy z nich wypowiada imię tego, który stoi najbliżej niego. Imiona Paweł i Zbyszek zostały powiedziane po dwa razy, imię Mirek raz. Wtedy
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #21
Marek zbudował prostopadłościan z 3 różnie pomalowanych klocków, z których każdy jest utworzony z 4 małych sześcianów. Potem jeden klocek został wyjęty (patrz rysunek). Który?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #22
W prostokącie ABCD punkty P, Q, R, S są odpowiednio środkami boków AS, SC, CD i DA. Niech T będzie środkiem odcinka SR. Jaką częścią pola prostokąta ABCD jest pole trójkąta PQT?
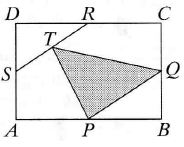

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #23
Ada zbudowała przedstawioną na rysunku obok figurę z figurek trójkwadratowych i czterokwadratowych obracając te figurki, ale ich nie przewracając. Ilu co najmniej figurek trójkwadratowych mogła użyć?
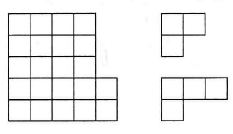
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #24
Na rysunku boki czterych nalegających kwa dratów wynoszą 11, 9, 7 i 5. Jaka jest róż nica pomiędzy łącznym polem obszarów za cieniowanych i łącznym polem obszarów po malowanych na czarno?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #25
Na półce ustawiono 50 książek, z których każda jest albo podręcznikiem matematyki, albo podręcznikiem fizyki. Żaden podręcznik fizyki nie stał obok innego podręcznika fizyki, ale obok każdego podręcznika matematyki stał przynajmniej jeden podręcznik matematyki. Które z poniższych zdań może być fałszywe?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #26
Kwadrat podzielony został na 25 identycznych kwadracików (patrz rysunek). Jaka jest suma miar kątów ∠MAN, ∠MBN, ∠MCN, ∠MDN и ∠MEN.

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #27
Trójkąt równoramienny ВАС (oznaczony na rysunku obok numerem 0) o kącie ВАС równym 100° obracamy wokół punktu A w kierunku przeciwnym do ruchu wskazówek zegara tak, aż powstanie trójkąt 1 mający z trójkątem 0 wspólne ramię. Następnie w ten sam sposób obracamy trójkąt 1, otrzymując trójkąt 2, potem obracamy trójkąt 2 otrzymując trójkąt 3 itd. Jaki jest najmniejszy dodatni numer trójkąta, który pokryje się z trójkątem 0?
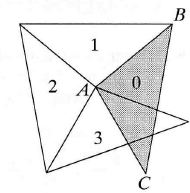
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #28
Ile liczb naturalnych n ma te własność, że reszta z dzielenia 2003 przez n jest równa 23?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #29
Na płaszczyźnie danych jest 10 punktów, z których żadne trzy nie leżą na jednej prostej. Każde dwa z tych punktów połączono odcinkami. Ile co najwyżej z tych odcinków można jednocześnie przeciąć jedna prostą, nie przechodzącą przez żaden z danych 10 punktów?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #30
W trójkącie ABC mamy: AB = АС, АЕ = AD, ∠BAD = 30°. Jaka jest miara kąta CDE?
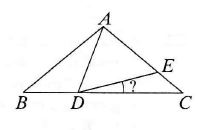
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5





