Konkurs z matematyki "Kangura" - 2009 - KADET - Litwa
Klausimas #1
Która z poniższych liczb jest największa?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #2
W spotkaniu towarzyskim u Adama wzięło udział czterech chłopców i cztery dziewczyny. W czasie spotkania chłopcy tańczyli tylko z dziewczętami, a dziewczęta tylko z chłopcami. Po spotkaniu, na pytanie: „Z iloma różnymi osobami tańczyłeś w czasie spotkania?", chłopcy kolejno powiedzieli: 3, 1, 2, 2, natomiast trzy pierwsze dziewczęta podały liczby: 2, 2, 2. Z iloma chłopcami tańczyła czwarta dziewczyna?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #3
Gwiazda pokazana na rysunku obok, utworzona jest z 12 identycznych trójkątów równobocznych. Obwód gwiazdy jest równy 36 cm. Ile jest równy obwód zacieniowanego sześciokąta?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #4
Jacek w ramach przygotowań do konkursu Kangur postanowił rozwiązać po jednym zadaniu z kolejnych stron o numerach nieparzystych w swoim zbiorze zadań. Rozpoczął na stronie 15, a skończył na stronie 53. Ile zadań treningowych rozwiązał Jacek?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #5
Duży kwadrat о polu 1 został podzielony na kwadraty, jak na rysunku obok. Pole małego czarnego kwadratu jest równe
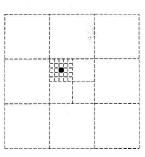
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #6
Iloczyn czterech różnych dodatnich liczb całkowitych jest równy 100. Suma tych liczb jest równa
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #7
W pokoju bawią się koty i psy. Liczba kocich łap jest dwa razy większa niż liczba psich nosów. Liczba kotów jest
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #8
Na rysunku obok punkty Q, S, R są współliniowe oraz P QPS = 12° i PQ = PS = RS. Wówczas miara kąta QPR jest równa
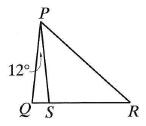
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #9
Mama przygotowała na zimę sok wiśniowy, którym można napełnić dokładnie 12 dużych słoików albo dokładnie 20 mniejszych słoików. Mama napełniła już 9 dużych słoików i resztę postanowiła rozlać do mniejszych słoików. Ile takich słoików napełni pozostałym sokiem?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #10
O godzinie 6:15 zniknął duszek Kacperek i w tym momencie szalony zegar, który dotychczas pokazywał prawidłową godzinę, zaczął chodzić z prawidłową prędkością, ale wstecz. Duszek pojawił się z powrotem o 19:30. Którą godzinę pokazywał szalony zegar w momencie powrotu Kacperka?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #11
Ile jest liczb całkowitych dodatnich, których kwadrat i sześcian mają tę samą liczbę cyfr?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #12
Jaka jest minimalna liczba pogrubionych punktów, które należy usunąć z rysunku, aby żadne trzy punkty spośród pozostałych nie leżały na jednej prostej?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #13
Mirek zmierzył wszystkie kąty w dwóch trójkątach. Jeden z trójkątów był ostrokątny, a drugi rozwartokątny. Mirek zapamiętał miary czterech z tych kątów: 120°, 80°, 55° i 10°. Jaka jest miara najmniejszego kąta w trójkącie ostrokątnym?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #14
Jaką częścią największego kwadratu jest obszar zacieniowany?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #15
Wyspę zamieszkują prawdomówni i kłamcy. Prawdomówni zawsze mówią prawdę, a kłamcy zawsze kłamią. 25 mieszkańców tej wyspy ustawiło się w kolejkę. Każda osoba z kolejki, z wyjątkiem pierwszej, powiedziała: Osoba stojąca bezpośrednio przede mną to kłamca, natomiast osoba stojąca jako pierwsza w kolejce powiedziała: Wszyscy stojący za mną to kłamcy. Ilu kłamców stało w tej kolejce?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #16
Powierzchnia bryły narysowanej obok składa się z 6 ścian trój- \ kątnych. W każdym wierzchołku bryły umieszczono liczbę tak, by sumy liczb umieszczonych w wierzchołkach danej ściany były jednakowe dla wszystkich ścian. Dwie liczby, 1 i 5, są zaznaczone na rysunku. Ile wynosi suma wszystkich liczb umieszczonych w wierzchołkach?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #17
W równości
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #18
Planujemy pokolorować kratki kwadratu, używając kolorów a, b, c i d w taki sposób, by żadne dwie kratki o wspólnym boku lub wierzchołku nie były pokolorowane tym samym kolorem. Pewne kratki są już pokolorowane.

Jakie są możliwe pokolorowania kratki zacieniowanej?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #19
Na rysunku mamy dziewięciokąt foremny. Jaka jest miara kąta X?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #20
Na rysunku obok mamy trzy początkowe układanki. Ile jest potrzebnych białych kwadracików jednostkowych, aby ułożyć dziesiątą układankę w tym ciągu?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #21
Wśród poniższych czterech zdań o liczbie naturalnej n dwa są prawdziwe i dwa fałszywe:
Liczba n jest podzielna przez 5.
Liczba n jest podzielna przez 11.
Liczba n jest podzielna przez 55.
Liczba n jest mniejsza niż 10.
Wtedy liczba n może być
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #22
Ile jest liczb dziesięciocyfrowych, które można napisać przy użyciu cyfr 1, 2 i 3 tak, aby każde dwie sąsiednie cyfry w ich zapisach różniły się o jeden?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #23
Na osi liczbowej zaznaczono ułamki

Która z liter oznacza ułamek
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #24
Trzema cięciami zaznaczonymi na rysunku podzielono duży sześcian na osiem prostopadłościanów.
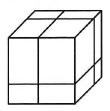
Ile jest równy stosunek sumy pól powierzchni tych ośmiu prostopadłościanów do pola powierzchni sześcianu?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #25
Ile jest liczb naturalnych n, dla których największy spośród jej dzielników naturalnych różnych od 1 i л jest 45 razy większy od najmniejszego spośród tych dzielników?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #26
Kwadrat podzielono na 2009 kwadratów, których długości boków są liczbami całkowitymi. Jaką najmniejszą długość może mieć bok dzielonego kwadratu?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #27
W czworokącie PQRS mamy PQ = 2006, QR = 2008, RS = 2007 i S P = 2009. Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż 180°?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #28
Mam kwadrat o wymiarach 6 cm x 6 cm i trójkąt. Jeżeli położę kwadrat na trójkącie, to mogę pokryć co najwyżej 60% powierzchni trójkąta. Jeśli zaś położę trójkąt na kwadracie, to mogę pokryć co najwyżej
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #29
Na kartce napisano w jednej linii kilka różnych liczb całkowitych dodatnich nie większych niż 10. Oglądając tę kartkę, Mirek stwierdził ze zdumieniem, że w każdej parze sąsiednich liczb jedna z nich dzieli drugą. Пе co najwyżej liczb mogło być napisanych na tej kartce?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #30
W trójkącie ABC miara kąta wewnętrznego przy wierzchołku В jest równa 20°, a miara kąta wewnętrznego przy wierzchołku С jest równa 40°. Ponadto długość dwusiecznej kąta przy wierzchołku A jest równa 2. Пе wynosi różnica ВС — AB?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1





