Konkurs z matematyki "Kangura" - 2009 - STUDENT - Litwa
Klausimas #1
W akwarium jest 200 rybek. 1% spośród nich jest koloru niebieskiego, pozostałe są żółte. Ile żółtych rybek należy przełożyć do innego akwarium, aby niebieskie stanowiły 2% rybek pozostawionych w akwarium?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #2
Która z poniższych liczb jest największa?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #3
Ile jest liczb naturalnych n takich, że liczba n2 + n jest pierwsza?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #4
Anabella, Beatrycze i Cecylia wybrały się do cukierni. Każda z nich zamówiła to samo: dwie szklanki soku, trzy porcje lodów i pączka. Poprosiły potem o wspólny rachunek. Jedna z poniższych liczb wyraża kwotę, która widniała na rachunku. Która?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #5
Powierzchnia bryły narysowanej obok składa się z 6 ścian trójkątnych. W każdym wierzchołku bryły umieszczono liczbę tak, by sumy liczb umieszczonych w wierzchołkach danej ściany były jednakowe dla wszystkich ścian. Dwie liczby, 1 i 5, są zaznaczone na rysunku. Ile wynosi suma wszystkich liczb umieszczonych w wierzchołkach?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #6
Dwa okręgi, jeden o promieniu 13, drugi o promieniu 15, przecinają się w punktach P i g, przy czym PQ = 24. Która z poniższych liczb może wyrażać odległość pomiędzy środkami tych okręgów?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #7
W pudelku są skarpetki: 2 białe, 3 czerwone i 4 niebieskie, przy czym jedna trzecia wszystkich skarpetek jest dziurawa. Adam wyjmuje w ciemności skarpetki z pudełka. Ile co najmniej powinien ich wyjąć, aby mieć pewność, że wśród wyjętych skarpetek będą przynajmniej dwie niedziurawe w tym samym kolorze?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #8
Rysunek obok przedstawia dwa zewnętrznie styczne okręgi oraz kwadrat o boku długości 1. Jeden z wierzchołków kwadratu pokrywa się ze środkiem większego okręgu, a dwa inne leżą na tym okręgu. Mniejszy okrąg jest styczny do dwóch boków kwadratu. Ile jest równy promień niniejszego okręgu?
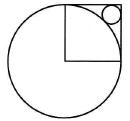
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #9
Boki trójkąta ABC przedłużono w obie strony do punktów P, Q, R, S, T, U w taki sposób, że PA = AB = BS, TC = CA = AQ, U С = С В = BR. Ile jest równe pole sześciokąta PQRSTU, jeżeli pole trójkąta ABC jest równe 1?
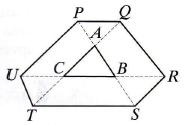
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #10
Planujemy pokolorować kratki kwadratu, używając kolorów a, b, c i d w taki sposób, by żadne dwie kratki o wspólnym boku lub wierzchołku nie były pokolorowane tym samym kolorem. Pewne kratki są już pokolorowane (patrz rysunek). Jakie są możliwe pokolorowania kratki zacieniowanej?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #11
W narożniku A kwadratowego stołu bilardowego o boku długości 2 m umieszczono bilę, którą następnie wprawiono w ruch. Bila, po odbiciu się od trzech band stołu, trafiła do narożnika В - patrz rysunek obok. Tle metrów przebyła bila na stole? (Pamiętajmy, że kąt, pod którym bila odbija się od bandy, jest równy kątowi, pod którym uderza w bandę.)

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #12
2009 kangurów, każdy albo jasny, albo ciemny, porównywało swój wzrost. Okazało się, że tylko jeden jasny kangur jest wyższy od dokładnie 8 ciemnych kangurów, tylko jeden jasny kangur jest wyższy od dokładnie 9 ciemnych kangurów, tylko jeden jasny kangur jest wyższy od dokładnie 10 ciemnych kangurów, itd., wreszcie tylko jeden jasny kangur jest wyższy od wszystkich ciemnych kangurów. Ile było jasnych kangurów?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #13
Z czterech ciemnych (nieprzezroczystych) i czterech przezroczystych sześcianików o wymiarach 1x1x1 można utworzyć sześcian o wymiarach 2x2x2, który jest całkowicie nieprzezroczysty, gdy patrzymy na niego w kierunku prostopadłym do dowolnej ściany (patrz rysunek obok). Be co najmniej takich ciemnych sześcianików należy użyć do budowy sześcianu o wymiarach 3x3x3, aby miał on tę samą własność?
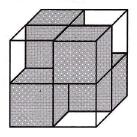
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #14
Wyspę zamieszkują prawdomówni i kłamcy. Prawdomówni zawsze mówią prawdę, a kłamcy zawsze kłamią. 25 mieszkańców tej wyspy ustawiło się w kolejkę. Każda osoba z kolejki, z wyjątkiem pierwszej, powiedziała: Osoba stojąca bezpośrednio przede mną to kłamca, natomiast osoba stojąca jako pierwsza w kolejce powiedziała: Wszyscy stojący za mną to kłamcy. Ilu kłamców stało w tej kolejce?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #15
Ostatnia cyfra liczby, która jest wynikiem działania 12 — 22 + 32 — 42 + ... — 20082 + 20092, jest równa
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #16
Na trójkąt równoboczny o boku długości 3 nałożono koło o pro¬, mieniu 1 w taki sposób, że środek koła pokrył się ze środkiem
ciężkości trójkąta. Uzyskana figura, której brzeg zaznaczono pogrubioną linią ciągłą, przedstawiona jest na rysunku obok. Ile jest równy obwód tej figury?
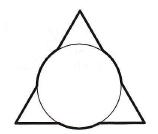
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #17
Rysunek obok przedstawia wykresy funkcji у = fix) oraz у = g(x). Jaki jest związek pomiędzy tymi funkcjami?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #18
100 uczestników konkursu matematycznego otrzymało do rozwiązania po cztery zadania. Okazało się, że pierwsze zadanie rozwiązało 90 uczestników, drugie 85, trzecie 80 i czwarte 70 uczestników. Największa możliwa liczba uczestników, o których możemy, korzystając z tych informacji, z pewnością orzec, że rozwiązali wszystkie zadania, jest równa
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #19
Na zamieszczonym obok rysunku, po lewej stronie linii przerywanej, przedstawiony jest widok od strony południowej (p.) i widok z góry (g.) pewnej budowli. Która z figur I, П, Ш, IV przedstawia widok tej budowli od strony zachodniej?
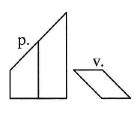
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #20
Tablicę kwadratową o wymiarach 3x3 wypełniono liczbami w taki sposób, że suma liczb w każdej kolumnie, w każdym wierszu i na każdej przekątnej jest taka sama. Dwie z tych liczb ujawniono na rysunku obok. Jaka liczba jest zacieniowana?
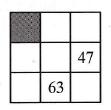
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #21
Ambroży i Bonifacy biegają wokół stadionu, każdy ze stałą prędkością. Ambroży, który biegnie szybciej niż Bonifacy, okrąża stadion w czasie 3 minut. Obaj wystartowali jednocześnie, z tego samego punktu i w tym samym kierunku. Po upływie 8 minut Ambroży po raz pierwszy zdublował Bonifacego. W jakim czasie Bonifacy pokonuje jedno okrążenie?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #22
Niech m oznacza liczbę wszystkich tych liczb 8-cyfrowych, w których żadne dwie cyfry nie powtarzają się i żadna cyfra nie jest równa 0. Ile takich liczb dzieli się przez 9?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #23
Ile jest liczb dziesięciocyfrowych, które można napisać przy użyciu cyfr 1, 2 i 3 tak, aby każde dwie sąsiednie cyfry w ich zapisach różniły się o jeden?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #24
Dla ilu liczb naturalnych n > 3 istnieje n-kąt wypukły, którego miary kątów, wziętych w odpowiednim porządku, są w stosunku 1:2:3:...:n?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #25
W konkursie matematycznym uczestniczyło 55 uczniów. Jurorzy sprawdzający zadania stawiali przy każdym poprawnie rozwiązanym zadaniu znak „+", przy każdym niepoprawnie rozwiązanym zadaniu znak „—", a znak „0", gdy uczestnik zadanie pominął. Po zakończeniu konkursu okazało się. że każde dwie prace różnią się liczbą znaków „+" lub liczbą znaków „—". Jaka jest najmniejsza liczba zadań, przy której jest to możliwe?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #26
W prostokącie JKLM dwusieczna kąta К JM przecina przekątną KM w punkcie N.
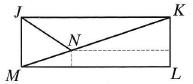
Odległość punktu N od boku LM jest równa 1, a od boku K L jest równa 8. Ile wynosi długość boku LM?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #27
Niech
Ile różnych wartości może przyjąć к?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #28
Liczby naturalne od 1 do 99 włącznie należy rozmieścić w n grupach (grupa - to nie mniej niż 2 liczby) tak, by spełniony był taki warunek:
jeśli dwie liczby są w tej samej grupie, to ich suma nie jest podzielna przez 3. Najmniejsza liczba n, dla której można to zrobić, jest równa
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #29
Na kartce napisano w jednej linii kilka różnych liczb całkowitych dodatnich nie większych niż 10. Oglądając tę kartkę, Mirek stwierdził ze zdumieniem, że w każdej parze sąsiednich liczb jedna z nich dzieli dragą. Ile co najwyżej liczb mogło być napisanych na tej kartce?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #30
Ciąg liczb (a„) zdefiniowano następująco:
a0=1, a1=2, an+2 = an + (an+1)2 dla n ≥ 0.
Reszta z dzielenia #2009 przez 7 jest równa
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1





