Konkurs z matematyki "Kangura" - 2012 - Kadet - Litwa
Klausimas #1
Cztery jednakowe czekolady kosztują o 6 złotych więcej niż jedna taka czekolada. Ile kosztuje jedna taka czekolada?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #2
11,11 - 1,111 =
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #3
Zegarek ze wskazówkami położono na stole tarczą do góry w taki sposób, że wskazówka minutowa wskazuje dokładnie kierunek wschodni. Po ilu minutach wskazówka ta po raz pierwszy wskaże dokładnie kierunek północny?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #4
Maciek ma nożyczki i pięć liter z tektury. Każdą z nich przecina jeden raz cięciem wzdłuż linii prostej tak, aby rozpadła się na możliwie największą liczbę części. Z której litery Maciek otrzyma najwięcej części?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #5
Smok ma pięć głów. Za każdym razem, gdy zetniemy jego głowę, wyrasta mu natychmiast pięć nowych głów. Ile głów będzie miał ten smok, jeśli zetniemy po kolei sześć jego głów?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #6
W poniższych wyrażeniach występuje tylko liczba 8. W którym z nich możemy zamienić każdą występującą liczbę 8 na jedną i tę samą, dowolnie wybraną, liczbę dodatnią tak, aby otrzymać ten sam wynik?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #7
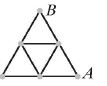
Każda z 9 ścieżek w parku (rysunek obok) ma 100 metrów. Julka chce przejść z punktu A do punktu B, nie idąc żadną ścieżką więcej niż raz. Ile metrów ma najdłuższa droga, którą może wybrać?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #8
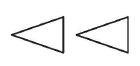
Na rysunku obok przedstawiono dwa trójkąty. Na ile sposobów można wybrać dwa wierzchołki, po jednym w każdym trójkącie, tak aby prosta przechodząca przez te wierzchołki nie rozcinała żadnego z tych trójkątów?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #9
Jasio złożył kartkę papieru na pół, jak pokazano na rysunku, a następnie wykonał nożyczkami dwa cięcia wzdłuż linii prostych. Którego z poniższych kształtów nie może w ten sposób otrzymać?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #10
Bryła przedstawiona na rysunku jest utworzona z czterech części. Każda z tych części składa się z czterech sześcianów i jest jednego koloru. Jaki kształt ma biała
część?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #11
Z cyfr 1, 2, 3, 4, 5, 6, 7, 8, używając każdej z nich dokładnie raz, utworzono dwie liczby czterocyfrowe o możliwie najmniejszej sumie. Jaka jest wartość tej najmniejszej sumy?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #12
Ogrodnik uprawia na grządce ogórki i truskawki. W tym roku wydłużył o 3 metry krótszy bok prostokątnej części przeznaczonej pod uprawę ogórków, wskutek czego ta część ma teraz kształt kwadratu. W ten sposób pole części obsadzonej truskawkami zmniejszyło się o 15m2. Przed tą zmianą pole części obsianej ogórkami było równe

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #13
Basia chce wstawić do tabeli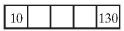 trzy liczby, po jednej w każde puste pole, tak, aby suma pierwszych trzech liczb była równa 100, suma trzech środkowych była równa 200, a suma trzech ostatnich była równa 300. Jaką liczbę powinna Basia wstawić w środkowe pole tabeli?
trzy liczby, po jednej w każde puste pole, tak, aby suma pierwszych trzech liczb była równa 100, suma trzech środkowych była równa 200, a suma trzech ostatnich była równa 300. Jaką liczbę powinna Basia wstawić w środkowe pole tabeli?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #14
Figurę przedstawioną na rysunku nazywamy pięciokątem gwiaździstym. Jaka jest miara kąta x?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #15
Trzy trójkąty równoboczne o tym samym boku odcięto w narożach dużego trójkąta równobocznego o boku 6 cm. Suma obwodów tych trzech małych trójkątów jest równa obwodowi pozostałego szarego sześciokąta. Jaka jest długość boku małych trójkątów?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #16
Ser pocięto na małe kawałki. Myszy wynosiły te kawałki, biorąc za każdym razem po jednym. Leniwy kot Mruczek zauważył, że każda mysz zebrała mniej niż 10 kawałków, przy czym każda inną ich liczbę, a ponadto żadna mysz nie zebrała dwa razy więcej kawałków niż inna mysz. Jaka jest największa możliwa liczba myszy, które mogły wynosić ten ser?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #17
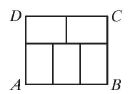
Prostokąt ABCD podzielono na 5 przystających prostokątów - patrz rysunek. Obwód każdego z tych 5 prostokątów jest równy 20 cm. Oblicz pole prostokąta ABCD.
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #18
Gadający kwadrat miał na początku bok długości 8 cm. Jeśli kwadrat mówi prawdę, każdy jego bok skraca się o 2 cm, a jeśli kwadrat kłamie, każdy jego bok się podwaja. Kwadrat wypowiedział cztery zdania, z których dwa były prawdziwe, a dwa fałszywe, ale nie wiemy w jakiej kolejności. Jaki jest największy możliwy obwód kwadratu po wypowiedzeniu takich czterech zdań?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #19
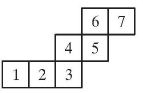
Kasia toczy sześcienną kostkę po macie pokazanej obok, startując z pola o numerze 1. Za każdym razem obraca kostkę wokół jednej z krawędzi. Kostka przylegała do maty kolejno w miejscach oznaczonych numerami: 1, 2, 3, 4, 5, 6 i 7. W których z tych miejsc kostka przylegała do maty tą samą ścianą?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #20
Na czterech kartach napisano liczby: 2, 5, 7 i 12, po jednej liczbie na każdej karcie. Na drugich stronach tych kart napisano określenia: „liczba podzielna przez 7", „liczba pierwsza", „liczba nieparzysta", „liczba większa od 100", po jednym na każdej karcie. Wiadomo, że na każdej z kart określenie nie pasuje do liczby napisanej na odwrocie. Która liczba jest na karcie z napisem „liczba większa od 100"?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #21
Zbyszek ma 5 sześcianów. Gdy ułoży je od najmniejszego do największego, to wysokości każdych dwóch sąsiednich sześcianów różnią się o 2 cm. Wysokość największego sześcianu jest równa wysokości wieży zbudowanej z dwóch najmniejszych sześcianów. Jaka jest wysokość wieży zbudowanej z wszystkich 5 sześcianów?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #22
Wyznacz stosunek pola trójkąta MNC do pola kwadratu ABCD, gdzie £) M jest środkiem boku AD, punkt N leży na przekątnej AC, a odcinek MN jest prostopadły do AC.

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #23
Tango tańczy się w parach - kobieta z mężczyzną. Na wieczorku tanecznym było nie więcej niż 50 osób. W pewnym momencie okazało się, że | mężczyzn tańczy tango z | kobiet. Ile osób wtedy tańczyło tango na sali?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #24
Paweł chce ustawić dwanaście liczb od 1 do 12 na okręgu w taki sposób, aby sąsiednie liczby zawsze różniły się o 2 lub o 3. Które z podanych liczb muszą ze sobą sąsiadować?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #25
Niektóre liczby trzycyfrowe mają następujące dwie własności:
• po usunięciu pierwszej cyfry otrzymujemy liczbę dwucyfrową będącą kwadratem liczby naturalnej,
• po usunięciu ostatniej cyfry otrzymujemy liczbę dwucyfrową będącą kwadratem liczby naturalnej.
Ile wynosi suma wszystkich takich liczb trzycyfrowych?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #26
W książce jest 30 opowiadań. Każde z nich zajmuje inną liczbę stron, od 1 do 30. Każde opowiadanie zaczyna się na nowej stronie, przy czym pierwsze opowiadanie zaczyna się na pierwszej stronie. Jaka jest największa możliwa liczba opowiadań, które mogą zaczynać się na nieparzystej stronie?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #27
Trójkąt równoboczny obracamy wokół jego środka: najpierw o 3°, potem o 9°, następnie o 27°, i tak dalej, tzn. w w-tym kroku obracamy o (3n)°. Ile różnych położeń będzie zajmował dany trójkąt (wliczając wyjściowe położenie)?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #28
Linę złożono na pół, potem znowu na pół, i jeszcze raz na pół. Następnie przecięto w jednym miejscu całą złożoną linę. Pewne dwa z otrzymanych kawałków są długości 9 i 4 metrów. Długość całej liny
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #29
Trójkąt o obwodzie 19 jest podzielony trzema odcinkami na cztery trójkąty i trzy czworokąty w sposób przedstawiony na rysunku. Suma obwodów czterech trójkątów jest równa 20, a suma obwodów trzech czworokątów jest równa 25. Ile jest równa suma długości trzech odcinków dzielących w ten sposób trójkąt?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #30
Kwadrat 3x3 podzielono na kwadraty jednostkowe. W każdym z nich wpisano liczbę dodatnią w taki sposób, że iloczyn liczb w każdym wierszu i w każdej kolumnie jest równy 1, a w każdym kwadracie 2x2 iloczyn liczb jest równy 2. Jaką liczbę wpisano w środkowym kwadracie?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5





