Math competition "Kangaroo" - 2003 - Cadet - Lithuania
Klausimas #1
There were 5 parrots in a pet shop. Their average price was 6000 dollars. One day the most expensive parrot was sold. The average price of the remaining four parrots was 5 000 dollars. What was the price (in dollars) of the parrot sold?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #2
A folded napkin was cut through (see picture). What does it look like when unfolded?
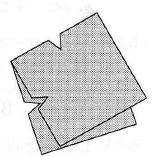
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #3
A straight line is drawn aeross a 4 x 4 chessboard. What is the greatest number of 1 x
sąuares which сап be cut into two pieces by the line?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #4
The area of the wooden square equals a. The area of each wooden circle equals b. Three
circles are lined up as shown in the picture. I f we tie together the three circles with a thread
as short as possible, without moving them, what is the area inside the thread?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #5
For a hexagon (not necessarily convex), the maximum possible number of interior right angles is
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #6
A bottle and a glass together have the same volume as a jug. A bottle has the same volume as a glass and a tankard. Three tankards have the same volume as two jugs. How many glasses of water equal one tankard?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #7
The composite board shown in the picture consists of 44 fields 1x1. How many possibilities are there to cover all 40 white fields with 20 rectangular stones 1x2? (The board cannot be turned. Two possibilities are different if at least one stone lies i n another way.)

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #8
In a positive integer consisting of at least 2 digits, the last digit has been crossed out, so that the number has been decreased n times. What is the maximum value of n?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #9
There are four line segments drawn. Which number of intersection points is impossible?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #10
Which of the following numbers gives, when multiplied by 768, the product ending with the highest number of zeroes?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #11
Lying on a table, there is a transparent square sheet of film with the letter У written on it. We turn the sheet 90° clockwise, then turn it over from its right side, then turn it 180° counterclockwise. What do we now see?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #12
Mike has 42 identical cubes, each with the edge 1 cm long. He used all of the cubes to construct a cuboid. The perimeter of the base of that cuboid is 18 cm. What is its height?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #13
Jeffrey shoots three arrows at each of four identical targets. He scores 29 points on the first target, 43 on the second and 47 on the third. How many points does Jeffrey score on the last target?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #14
The weight of a truck without a load is 2000 kg. Today the load initially comprised 80% of the total weight. At the first stop, a ąuarter of the load was left. What percentage of the total weight does the load then comprise?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #15
Two ąuadrates with the same size cover a circle, the radius of which is 3 cm. Find the total area (in cm2) of the shaded figure.

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #16
You have six line segments of lengths 1 cm, 2 cm, 3cm, 2001 cm, 2002 cm and 2003 cm. You have to choose three of these segments to form a triangle. How many different choices of three segments are there which work?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #17
How many positive integers n possess the following property: among the positive divisors of n different from 1 and n itself, the largest is 15 times the smallest.
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #18
Six points K, L, M, N, P, R are marked on a line from left to right, in the same order as listed. It is known that KN = MR and LN = NR. Then, necessarily
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #19
Mary has 6 cards with natūrai numbers written on them (one number on each card). She chooses 3 cards and calculates the sum of the corresponding numbers. Having done this for all 20 possible combinations of 3 cards, she discovers that 10 sumš are eąual to 16, and the other 10 sumš are eąual to 18. Then the smallest number on the cards is
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #20
Paul, Bill, John, Nick and Tim stood in a circle, the distances between any two neighbours being different. Each of them said the name of the boy standing elosest to him. The names Paul and Bill were said two times each, and the name John was said once. Then
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #21
A rectangular parallelepiped was composed of 3 pieces, each consisting of 4 little cubes. Then one piece was removed (see picture). Which one?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #22
In a rectangle ABCD, let P, Q, R and S be the midpoints of sides AB, ВС, CD and AD, respectively, and let T be the midpoint of segment RS. Which fraction of the area of ABCD does triangle PQT cover?
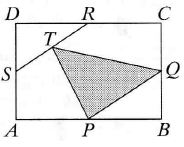
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #23
Carl composed the figure shown on the left side of the drawing from the smaller three-square and four-square figures shown on the right side. The smaller figures can be turned around, but not turned over. What is the smallest number of three-square figures needed for that?
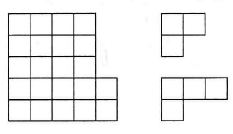
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #24
In the picture there are four overlapping squares with sides 11, 9, 7 and 5 long. How much greater is the sum of the two grey areas than the sum of the two black areas?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #25
On a bookshelf there are 50 math and physics books. No two physics books stand side by side, but every math book has a math neighbour. Which of the following statements may turn out to be false?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #26
A sąuare is divided into 25 small squares (see the picture). Find the measure of the angle which is the sum of the angles MAN, MBN, MCN, MDN, MEN.

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #27
We are going to make a spiral of isosceles triangles. We'11 start with the shaded triangle ВАС, which has a top angle AB AC = 100°, and move counterclockwise. Let AABC have number 0. Every of the next triangles (with numbers 1, 2, 3,...) will have exactly one edge adjoining the previous one (see the picture). What will be the number of the first triangle which precisely covers triangle nr. 0?
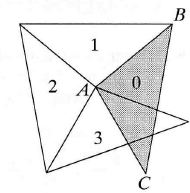
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #28
How many positive integers n сап be found such that 2003 divided by и leaves a remainder of 23?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #29
There are some 10 points on the area, and there are no three points on the same line. Every two points are connected by a segment. What is the largest possible number of these segments, which сап be crossed by another line that doesn't pass through any of these points?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #30
In triangle ABC (see picture) AB = AC, AE = AD, and ∠BAD = 30°. What is the measure of angle CDE?
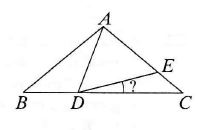
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5





