Math competition "Kangaroo" - 2004 - Cadet - Lithuania
Klausimas #1
What is the value of 2004 - 200 • 4?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #2
An equilateral triangle ACD is rotated counterclock-wise around point A. At what angle has it been rotated unen it covers equilateral triangle ABC for the first time?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #3
We multiplied the number x by 0.5 and divided the product obtained by 3. By squaring the quotient and adding 1 we obtained 50. What is the number x equal to?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #4
Caroline wants to write the numbers 1, 2, 3, 4 in the square 4 x 4 in such a way that every row and every column has each of the numbers. You see how she started. How many of the 4 numbers can be written in place of xl
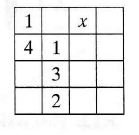
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #5
The value of the expression (1 - 2) - (3 - 4) - (5 - 6)- . . . - (99 - 100) is equal to
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #6
The section of a cube by a plane generates a plane figurę. I have plotted this section in the development of the cube (see the picture). Can you find out what figurę it is?
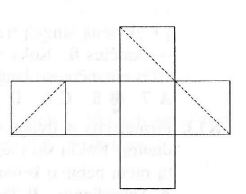
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #7
We have a rectangle and decide to enlarge it by increasing both length and width by 10% .The percentage of increase in area is
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #8
The point O is the center of the circle in the picture.What is the diameter of the circle?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #9
An ice cream stand has five different flavors. A group of children comes to the stand, and each child buys a double scoop eone with two flavors of ice cream. If none of the children choose the same combination of flavors, and every different combination of flavors is chosen, how many children are there?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #10
We link rings together as shown in the figurę below; the length of the chain is 1.7 m.

How many rings are there?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #11
In the picture a sąuare ABCD and two semicircles with diameters AB and AD have been drawn. If AB = 2, what is the area of the shaded region?
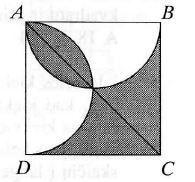
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #12
In the picture we have 11 fields.
In the first field there is a 7, and in the ninth field we have a 6. What positive integer has to be written in the second field for the following condition to be valid: the sum of any three adjoining fields is equal to 21?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #13
In the first year of two consecutive years there were more Thursdays than Tuesdays. Which day of the week was there more of in the second year, considering that neither of these years was a leap year?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #14
ABC is an isosceles triangle with AB = AC = 5 cm and ∠BAC > 60°. The length of its perimeter is a whole number of centimeters. How many such triangles are possible?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #15
Romeo the ostrich is training for the Head in the Sand Competition. He put his head into the sand at 8:15 on Monday morning and having been underground for 98 hours and 56 minutes reached a new personai record. When did Romeo puli his head out of the sand?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #16
Somebody has a large amount of building bricks 1 x 2 x 3. What is the smallest number of bricks needed to build a cube?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #17
Each of five children thinks of a number, which can be either 1, 2, or 4. Their numbers are multiplied. Which number could be the result?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #18
The average age of grandmother, grandfather, and 7 grandchildren is 28 years. The average age of 7 grandchildren is 15 years. Find the age of grandfather, if it is known that grandfather is 3 years older than grandmother.
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #19
There were more than two kangaroos in the enclosure. One kangaroo said, "There are 6 of us here," and jumped out of the enclosure. During each consecutive minute one kangaroo jumped out of the enclosure and said, "Everybody who jumped out before me was lying." It continued until there were no kangaroos in the enclosure. How many kangaroos told the truth?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #20
In a square with sides of length 6 the points A and B are on a line joining the midpoints of the opposite sides of the square (see the figurę). When you draw lines from A and B to two opposite vertices, you divide the sąuare in three parts of equal area. What is the length of AB?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #21
A woman goes from a city to the beach at 30 km/h. On the return trip her speed is 10 km/h. What is her average speed for the whole trip?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #22
John decided to put some of his magazines on his bookshelf. They have either 48 or 52 pages. Which one of these numbers cannot be the totai number of pages of the magazines on the bookshelf?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #23
You write a number in each square as shown in the square figurę. Then, the number x cannot be:

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #24
If a and b are positive integers, neither of which is divisible by 10, and if ab = 10,000, then the sum a + b equals
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #25
After one operation, the triplet (д, b, c) turns into triplet (b + c, c + a, a + b). After 2004 successive operations, the triplet (1,3, 5) turned into a triplet (x, y, z). What is the difference x — y equal to?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #26
This is a multiplication table. Which two letters represent the same number?
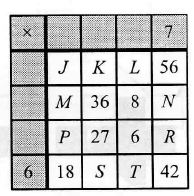
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #27
Some positive integers are written on the faces of a cube, and at each vertex we write the number eąual to the product of the numbers on the three faces adjacent to that vertex. The sum of the numbers at the vertices is 70. Then the sum of the numbers on the faces is:
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #28
The number 2004 is divisible by 12, and the sum of its digits is eąual to 6. Altogether, how many four-digit numbers have these two properties?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #29
A right triangle with legs of length 6 cm and 8 cm is cut out of a sheet of paper and then folded along a straight line. What can the area be, in cm2, of the resulting polygon"?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #30
In the Kangaroo summer camp a math competition was organized with 10 problems. Each correct answer was worth 5 points. For each incorrect answer 3 points were deducted. Everybody answered all the problems. Matt had 34 points, Zsolt had 10 points, and Gabor had 2 points. How many correct answers did they have altogether?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5





