Math competition "Kangaroo" - 2004 - Junior - Lithuania
Klausimas #1
The value of the expression (1 - 2) - (3 - 4) - (5 - 6)- . . . - (99 - 100) is eąual to
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #2
Edward has 2004 marbles. Half of them are blue, one ąuarter are red, and one sixth are green. How many marbles are of some other color?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #3
A pyramid has 7 faces. How many edges does it have?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #4
The ground plan of a building has a rectangular shape with parameters of 40 m x 60 m. In the diagram the ground plan of the building has a perimeter of 100 cm. What is the scale of the diagram?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #5
Tom and Ron both had some one-euro coins. When Tom got 5 more coins from his grandfather, he had twice as many coins as Ron. And if Tom now gave 12 coins to his grandmother, he would have half as many coins as Ron. How many coins did Tom have at the very beginning?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #6
Some angles in the quadrilateral ABCD are shown in thefigurę, ВС= AD, then what is the angle ADC ?
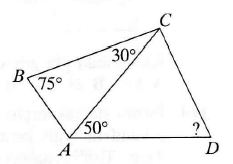
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #7
There are some boletuses and orange-caps in a basket - 30 mushrooms altogether. If we randomly take out 12 mushrooms, there will be at least one orange-cap among them. If we randomly take out 20 mushrooms, there will be at least one boletus among them. How many boletuses are there in the basket?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #8
In a square 2003 x 2003, the squares 1 x 1 on the diagonals are colored (like in the picture, where the square is 7 x 7). How many white squares are there?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #9
The dartboard shown consists of an inner black circle and 2 rings around it. The width of each ring is equal to the radius of the black circle. How many times greater is the area of the grey ring than the area of the inner black circle?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #10
After gathering 770 nuts, three girls divided them in proportion to their ages. For every 3 nutš Охапа took, Ira took 4. For every 7 nutš Natalya took, Ira took 6. How many nutš did the youngest girl get?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 3
Klausimas #11
Each of five children thinks of a number, which can be either 1, 2, or 4. Their numbers are multiplied. Which number could be the result?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #12
The circles with centers C and D meet at the points A and B, as shown. Angle ACB = 60° and angle ADB = 90°. How many times longer is the radius of the larger circle than the radius of the smaller circle?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #13
We link rings together as shown in the figurę below; the length of the chain is 1.7 m.

How many rings are there?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #14
In tank I, whose base has an area of 2 dm2 and whose height is 10 cm, the water is 5 cm high. An empty tank II with a base of area 1 dm2 and a height of 7 cm is placed in tank I. The water of tank I rises, of course, and spills over into tank II.
What level does the water reach in tank II?

Kokį lygį vanduo pasieks antrame inde?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #15
The hour hand of a clock is 4 cm long, and the minute hand is 8 cm long. What is the ratio of the distances travelled by the tips of the two hands between 2 pm and 5 pm?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #16
Three semi-circles, the diameters of two of which are equal to 4 and of the third to 8, are arranged as seen in the picture. What is the distance from the center S of the bigger semi-circle to the tangent point T of the smaller semi-circles?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #17
A quiz has twenty questions with seven points awarded for each correct answer, two points deducted for each wrong answer, and zero for each question omitted. Andrew scores 87 points. How many questions did he omit?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #18
Caroline wants to write the numbers 1, 2, 3, 4 in the square 4 x 4 in such a way that every row and every column has each of the numbers. You see how she started. In how many different ways can she finish?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #19
How many numbers exist between 100 and 200 which can have only the prime factors 2 and 3?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #20
The diagram shows two tangential circles with radii in the ratio 1:2. The smaller circle rolls around the inside of the large circle. Which of the following is the path traced out by the point P of the smaller circle?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 4
Klausimas #21
In a rectangle we draw both diagonals and the segment which joins a vertex with the midpoint of one of the sides, as shown in the picture. What is the result of dividing the length of the diagonal by the length of segment O PI

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #22
The real numbers a and b have different signs. Which of the numbers given below is the largest one?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #23
The diagram shows a square and an equilateral right-angled cross-shaped dodecagon. The length of the perimeter of the dodecagon is 36 cm. What, in cm2, is the area of the square?
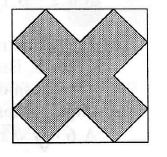
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #24
How many 3-digit numbers smaller than 200 have the property that the number (n+1)(n+ 2)(n + 3) is divisible by 7?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #25
A rectangle is divided into 4 triangles as shown in the figure. Of the following possibilities for the areas of the triangles at most one can be true. Which one is it?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #26
This is a multiplication table. Which two letters represent the same number?
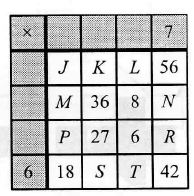
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #27
After one operation, the triplet (a, b, c) turns into triplet (b + c, c + a, a + b). After 2004 successive operations, the triplet (1, 3, 5) turned into a triplet (x, y, z). What is the difference x — y equal to?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #28
How many 8-digit numbers
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #29
The area of the shaded shape is equal to 2π.(see the picture). What is the value of the chord AB?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5
Klausimas #30
All the integers from 1 to 10,000 were written down on a blackboard. After that the numbers that are not divisible by 5 or 11 were erased. Then the 2004th element of the seąuence obtained was:
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 5





