Math competition "Kangaroo" - 2008 - Student - Lithuania
Klausimas #1
Numbers 3, 4 and two other unknown numbers are written in the cells of the 2x2 table. It is known that the sums of numbers in the rows are equal to 5 and 10, and the sum of numbers in one of the columns is equal to 9. The larger number of the two unknown ones is

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #2
If x + у=0 and х ≠ 0, then х2008 : у2008 =
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #3
An array contains 21 columns numbered 1, 2, ... 21, and 33 rows numbered 1, 2, ... 33. We erase the rows whose number is not a multiple of 3 and also the columns whose number is even. How many cells of the array remain after that?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #4
How many prime numbers p have the property that p4 + 1 is prime as well?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #5
A river starts at point A. As it flows the river splits into two. The first branch takes | of the water and the second takes the rest. Later the first branch splits into three, one taking | of the branch's water, the second | and the third one the rest. Further down this last branch meets again a branch of the river. The map below shows the situation.
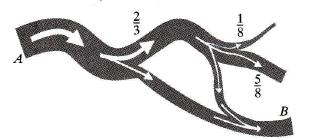
What part of the original water flows at point B?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #6
Given an isosceles triangle ABC, С A = CB, AD = = AC, DB = DC (see the fig.). Find the value of the angle ACB.
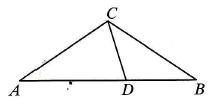
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #7
The maximum value f(x)= of |5sinx — 3|, x ∈ R, is
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #8
The figure shows a circle with the diameter A В and point D on it. Find d.
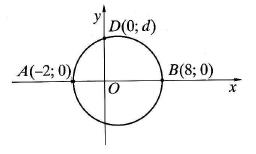
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #9
We have five different points A1, A2, A3, A4 and A5, arranged in this order on a straight line. Point P is placed on the same line so that the sum of the distances PA1 + PA2 + PA3 + +PA4 + PA5 were minimal. Then point P is
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #10
Nora wants to have two digits instead of the asterisks in 2** 8 such that the complete four-digit number were divisible by 3. How many possibilities are there?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #11
Here are seven numbers: -9, 0, -5, 5, -4, -1, -3. We arranged six of them in groups of two so that the sum in each group is the same. Which number remains free?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #12
Each of the cubes in the figure has the length of an edge equal to 1. What is the length of the segment AS?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #13
Five problems are proposed for a mathematical competition. Since the problems are of different difficulty level, no two of them have the same point value (all point values are positive integers). Bill solved all the five problems and he obtained a total of 10 points for two problems with the lowest point values and a total of 18 points for two problems with the highest point values. How many points did Bill obtain?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #14
Mathilde drew 36 kangaroos using three different colours. 25 of the kangaroos contain some yellow, 28 some brown, and 20 some black colour. Only 5 of them have all the three colours. How many single-colour kangaroos did she draw?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #15
If sinx + cosx = m, then sin4 x + cos4x =
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #16
In the figure the two regular hexagons are congruent. What part of the parallelogram's area is shaded?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #17
The numerator and denominator of a fraction are negative numbers, and the numerator is larger by one than the denominator. Which of the following is true about the fraction?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #18
Suppose x2yz3 = 73 and xy2 = 79. Then xyz =
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #19
We take three points from the grid so that they were col linear. How many possibilities do we have?
.jpg)
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #20
Four identical dice are arranged in a row (see the fig.). Each dice has faces with 1, 2, 3, 4, 5 and 6 points, but the dice are not standard, i.e., the sum of the points on the opposite faces of the dice is not necessarily equal to 7. What is the total sum of the points in all the 6 touching faces of the dice?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #21
The lengths of the edges of a block (rectangular parallelepiped) in centimetres are integers and they form a geometric progression with the quotient q = 2. Which of the following numbers can be the volume of this solid?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #22
In the figure each asterisk stands for one digit. The sum of the digits of the product is equal to

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #23
Find the value of the expression x2 + y2 + z2, if x + y + z = 1, and
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #24
A sequence is defined by a1 = 0 and an+1 = an + (-1)n • n, n ≥ 1. If ak = 2008, then the value of к is
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #25
A circle is inscribed in the triangle ABC (see the figure), AC = 5, AB = 6, ВС = 3. The segment ED is tangent to the circle. The perimeter of the triangle ADE is

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #26
The square ABCD has a side of length 1 and M is the midpoint of AB. The area of the shaded region is
.jpg)
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #27
Seven cards are in a box. The numbers from 1 to 7 are written on these cards. The first sage takes at random 3 cards out of the box and the second sage takes 2 cards (2 cards are left in the box). Then, looking at his cards, the first sage says to the second one: "I know that the sum of the numbers of your cards is even". What is the sum of card numbers of the first sage?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #28
We used metal rods to build this nice ensemble. We know there are 61 octagons. How many rods are there?
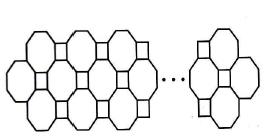
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #29
The number 332 - 1 has exactly two divisors which are larger than 75 and smaller than 85. What is the product of these two divisors?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #30
How many 2008-digit numbers there exist, in which every two-digit number composed of two sequential digits is divisible either by 17 or by 23?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1





