Math competition "Kangaroo" - 2009 - Cadet - Lithuania
Klausimas #1
Which of these numbers is even?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #2
There were 4 boys and 4 girls at a party. The boys danced only with girls and the girls danced only with boys. Afterwards we asked all of them, how many dance partners each of them had. The boys said: 3, 1, 2, 2. Three of the girls said: 2, 2, 2. What number did the fourth girl say?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #3
The star in the picture is formed from 12 identical small equilateral triangles. The perimeter of the star is 36 cm. What is the perimeter of the shaded hexagon?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #4
Harry delivers folders in the Long Street. He must deliver a folder to all the houses with an odd number. The first house has number 15, the last one has number 53. How many houses does Harry visit?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #5
The area of the big square is 1. What is the area of the black little square?
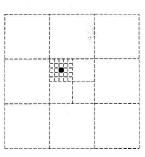
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #6
The product of four different positive integers is 100. What is their sum?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #7
There are cats and dogs in the room. The number of cats' paws is twice the number of dogs' noses. Then the number of cats is
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #8
In the figure on the right, QSR is a straight line, QPS = 12° and PQ = PS = RS. What is the size of QPR?
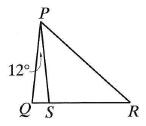
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #9
The elevator can take either 12 adults or 20 children. How many children at most could go up with 9 adults?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #10
At 6:15 a ghost vanished, and the mad clock that showed the right time so far, started running at the right speed, but backwards. The ghost appeared again at 19:30. What time did the mad clock show at the moment the ghost has appeared again?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #11
How many positive integers have as many digits in the decimal representation of their square as of their cube?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #12
What is the smallest number of bold points in the figure one needs to remove so that no 3 of the remaining points were collinear?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #13
Nick measured all the 6 angles in two triangles - one acute-angled and one obtuse-angled. He remembered four of those angles: 120°, 80°, 55°, and 10°. What is the smallest angle of the acute-angled triangle?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #14
Which part of the outer square is shaded?

Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #15
25 people are standing in a queue on the island of nobles and liars. Everyone, except the first person in the queue, said that the person ahead of him in the queue was a liar, and the first man in the queue said that all the people standing behind him were liars. How many liars were there in the queue? (Nobles always speak the truth, and liars always tell lies.)
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #16
The picture shows a soUd formed with 6 triangular faces. At each vertex there is a number. For each face we consider the sum of the 3 numbers at the vertices of that face.

If all the sums are the same and two of the numbers are 1 and 5, as shown, what is the sum of all the 5 numbers?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #17
In the equality
different letters stand for different digits while the same letters stand for the same digits. How many different values can the product THREE have?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #18
We want to color the squares in the grid using colors a, b, c, and d so that neighboring squares were not of the same color (squares that share a vertex are considered neighbors). Some of the squares have been colored as shown.

What are the possibilities for the shaded square?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #19
The diagram shows a regular enneagon (9-sided polygon).

What is the size of the marked angle at X?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #20
The first three patterns are shown.

How many white unit squares are needed to build the 10th pattern in this sequence?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #21
There are 4 statements about the positive integer M:
M is divisible by 5;
M is divisible by 11;
M is divisible by 55;
M is less than 10.
It is known that two of these statements are true, and the other two are false. Then M can be equal to:
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #22
How many ten-digit numbers, composed only of digits 1, 2, or 3, do there exist, in which any two neighboring digits differ by 1?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #23
The fractions

Where is the fraction
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #24
Three cuts are made through a large cube to get eight smaller cuboids.
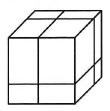
What is the ratio of the total surface area of these eight cuboids to the surface area of the original cube?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #25
All the divisors of number N, unequal to N and to 1, were written in turn. It occurred that the greatest of the divisors in the line is 45 times as great as the smallest one. How many numbers N satisfy this condition?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #26
A square has been dissected into 2009 squares whose lengths of the sides are integers. What is the shortest possible length of the side of the original square?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #27
In the quadrilateral PQRS, PQ = 2006, QR = 2008, RS = 2007 and S P = 2009. Which interior angles of the quadrilateral are necessarily smaller than 180°?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #28
If I place a 6 cm x 6 cm square on a triangle, I can cover up to 60% of the triangle. If I place the triangle on the square, I can cover up to | of the square. What is the area of the triangle?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #29
Man Friday wrote down in a row several different integers smaller than 11. Robinson Crusoe examined these numbers and noticed with satisfaction that in each pair of the neighbouring numbers one of the numbers was divisible by another. How many numbers at most could Man Friday write down?
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1
Klausimas #30
In a triangle ABC, the angle В is 20° and the angle С is 40°. The length of the bisector of the angle A is 2. Find ВС - AB.
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija
Taškų skaičius už teisingą atsakymą: 1





