Math competition "Kangaroo" - 2009 - Student - Lithuania

---

There are 200 fishes in an aquarium. 1% of them is blue, all the rest are yellow. How many yellow fishes do we have to take out of the aquarium, so that the blue fishes represented 2% of all the aquarium fishes?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Which is the largest of the following numbers?



Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

For how many different positive integers n the number n2 + n is a prime number?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Mari, Ville and Ossi went to a cafe. Each of them bought three glasses of juice, two icecreams, and five buns. Which of the following sums could be the total bill?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

The picture shows a solid formed with 6 triangular faces. At each vertex there is a number. For each face we consider the sum of the 3 numbers at the vertices of that face.

If all the sums are the same and two of the numbers are 1 and 5, as shown, what is the sum
of all the 5 numbers?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Two circles of radii 13 and 15 intersect at points P and Q. Length of line segment PQ is 24. Which of the following numbers could be the distance between the centers of circles?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

A box contains 2 white, 3 red and 4 blue socks. Jack knows that a third of the socks have a hole in them but he does not know what color the worn through socks are. In the darkness he takes some socks out of the box in a hope to find two good socks of the same color. How many socks must he take out to be absolutely sure to have a good pair?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

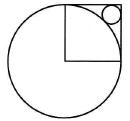
The square in the figure has a side equal to 1. Then the radius of the small circle is equal to



Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

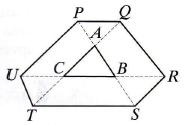
The sides of triangle ABC are extended on both sides up P Q to points P, Q, R, S, T and U so that PA = AB = BS, ТС = С A = AQ and UC = CB = BR. If the area of ABC is 1, what is the area of the hexagon PQRSTU?



Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

We want to color the squares in the grid using colors a, b, c, and d so that neighboring squares were not of the same color (squares that share a vertex are considered neighbors). Some of the squares have been colored as shown.

What are the possibilities for the shaded square?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

On a square-shaped billiard table with a side 2 m long, a ball is thrown from the corner A. After touching three sides, as shown, it rolls to corner B.How many meters did the ball travel? (Remember that a ball bounces at the same angle as it enters, as shown in the picture on the right.)



Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

2009 kangaroos, each of them either light or dark, compare their heights. It is known that one light kangaroo is taller than exactly 8 dark kangaroos, one light kangaroo is taller than exactly 9 dark kangaroos, one light kangaroo is taller than exactly 10 dark kangaroos, and so on, and exactly one light kangaroo is taller than all the dark kangaroos. What is the number of light kangaroos?



Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

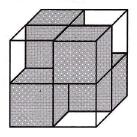
A cube measuring 2 x 2 x 2 is formed from four lxlxl white transparent and four lxlxl black non-transparent cubes (see the picture). They are placed so that the whole big cube is non-transparent, meaning that it is not possible to see through it neither from top to bottom, nor from front to back and even not from left to right. How many black cubes at least should we have to put into the big cube measuring 3 x 3 x 3 to make the whole cube non-transparent?



Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

25 people are standing in a queue on the island of nobles and liars. Everyone, except the first person in the queue, said that the person ahead of him in the queue was a liar, and the first man in the queue said that all the people standing behind him were liars. How many liars were there in the queue? (Nobles always speak the truth, and liars always tell lies.)


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

What is the last digit of the number l² - 2² + ... - 2008² + 2009²?



Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

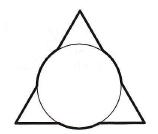
We overlap an equilateral triangle with the side length of 3 and a circle of radius 1 matching the centers of the two figures. How long is the perimeter of the figure that we get?



Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

The graphs of real functions / and g are shown in the figure. What is the relation between f(x) and g(x)?




Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Four problems were proposed to each of 100 contestants of a mathematical olympiad. 90 contestants solved the first problem, 85 contestants solved the second problem, 80 contestants solved the third problem, and 70 contestants solved the fourth problem. What is the smallest possible number of the contestants who solved all the four problems?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

In the figure below, you see the front view (f.) and the top view (t.) of a geometric solid. Which of the figures from I to IV represents the view from the left?



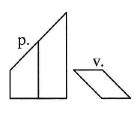
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

 We have constructed a 3 x 3-square table of real numbers in which the sum in each row, column, and diagonal is the same. Two of the numbers are shown in the figure. Which number is in the shaded square?



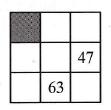
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Two runners A and В are running round a stadium. A runs faster than В and it takes 3 minutes to A for one lap. A and В started together, and 8 minutes later A caught В for the first time. How long does it take for В to ran one lap?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

 Let m be the number of 8-digit numbers with 8 different digits, none of which is 0. How many of them are divisible by 9?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

How many ten-digit numbers, composed only of digits 1, 2 and 3, do there exist, in which any two neighboring digits differ by 1?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

For how many integers n≥3 does there exist a convex n-gon whose angles in some order are in ratio 1 : 2 : ... : n?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

55 schoolchildren took part in math olympiad. When checking the problems, the jury marked them either by „+" if the problem was solved, or by „-" if the problem was not solved, or by „0" if participant skipped the problem. Later it turned out that no two papers had the same number of „+" and „-". What is the least number of problems at the olympiad?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

In a rectangle JKLM, the bisector of angle KJM cuts the diagonal KM at point N. The distances between N and sides LM and KL are 1 and 8, respectively. Then LM is:



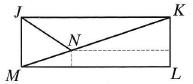
Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

If how many possible values of к are there?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

The numbers 1, 2, 3,..., 99 are distributed into n groups (at least 2 numbers in a group) under the condition:
if two numbers are in one and the same group, then their sum is not divisible by 3. The smallest n with this property is:


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

Man Friday wrote down in a row several different integers smaller than 11. Robinson Crusoe examined these numbers and noticed with satisfaction that in each pair of the neighbouring numbers one of the numbers was divisible by another. How many numbers at most could Man Friday write down?


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija

---

 The sequence of integers a_n is defined by:

The remainder in the division of a₂₀₀₉ by 7 is:


Atsakymų variantai rodomi tik registruotiems sistemos eTest.lt vartotojams. Mokytojo registracija, mokinio registracija